Para calcular limites algébricamente debemos aprender a racionalizar y a factorizar.

¿Cómo racionalizar?

Una fracción con raíces en el denominador, que consiste en operar para eliminar los radicales del denominador de una fracción. ​ Para ello se multiplica el numerador y el denominador por otra expresión de forma que, al operar, se elimine la raíz del denominador.

Ejemplo:

Racionalización de un monomio:

Para racionalizar un monomio de este tipo, se debe multiplicar el numerador y el denominador de la fracción por la raíz del denominador cuyo radicando se eleva a la diferencia entre el índice y el exponente. En el siguiente caso:

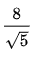
Hay que multiplicar numerador y denominador por √5:

Después se despeja la raíz cuadrada del denominador ya que la cantidad subradical que es 5 elevada al cuadrado puede eliminar o despejar la raíz cuadrada:

Racionalización de binomio:

Para racionalizar un binomio, se debe hacer un proceso similar al ejercicio anterior, multiplicar el numerador y denominador de la fracción por la expresión conjugada del denominador de la misma. En el siguiente ejemplo:

Hay que multiplicar el numerador y el denominador por √2 - √3; este resultado es el que da el producto notable de los binomios conjugados.

¿Cómo factorizar?

Cuando hablamos de factorizar, podemos seguir las siguientes recomendaciones:

• Observar si hay un factor común, esto es, si hay un factor que se repita en los diferentes términos.
• Ordenar la expresión: a veces al arreglar la expresión nos percatamos de las posibilidades de factorización.
• Averiguar si la expresión es factorizable: en ocasiones estamos en presencia de expresiones que no pueden ser descompuestas en factores.
• Verificar si los factores hallados son a su vez factorizables.

Factorizar una ecuación cuadrática:

Cuando tenemos un polinomio de tres términos, este puede ser un trinomio cuadrático de la forma ax2+bx+c. Esta expresión se obtiene de la multiplicación de dos binomios:

Al factorizar una ecuación cuadrática como  , queremos conseguir los dos binomios que lo originaron: (x+7)(x+2). 

Factorización de binomios:

Los binomios factorizables son:

• la diferencia de dos cuadrados (x²-y²),
• la diferencia de dos cubos(x³-y³) y
• la suma de dos cubos (x³+y³).

La factorización de la diferencia de dos cuadrados (x²-y²) es:

Ejemplo:

La factorización de la diferencia de dos cubos (x³-y³) es:

Ejemplo:

La factorización de la suma de dos cubos (x³+y³) es:

Ejemplo:

Productos Notables:

Cuadrado de la suma de dos cantidades:

(a + b) ^ 2

Cuando tenemos dos cantidades a y b, cuya suma está elevada al cuadrado, lo que realmente se pide es que se multiplique la suma por si misma:

(a + b) ^ 2 = (a + b)(a + b)

Esta multiplicación se efectúa de la siguiente forma:

(a + b) * (a + b) = a * a + a * b + b * a + b * b =

a ^ 2 + 2ab + b ^ 2

Ejemplos con solución paso a paso

 -Desarrollemos (x+10)².

• Cuadrado del primer término: x².
• Dos veces el primero por el segundo: 2(x)(10)=20x.
• Cuadrado del segundo término: 10²=100.

Respuesta:

¡¡Gente nos vemos en la siguiente publicación donde aprenderemos a calcular limites algebraicamente!!

Saludos.